7  Introduction to Design of Experiments (DoE)

Author
Affiliation

Prof. Dr. Tim Weber

Deggendorf Institute of Technology

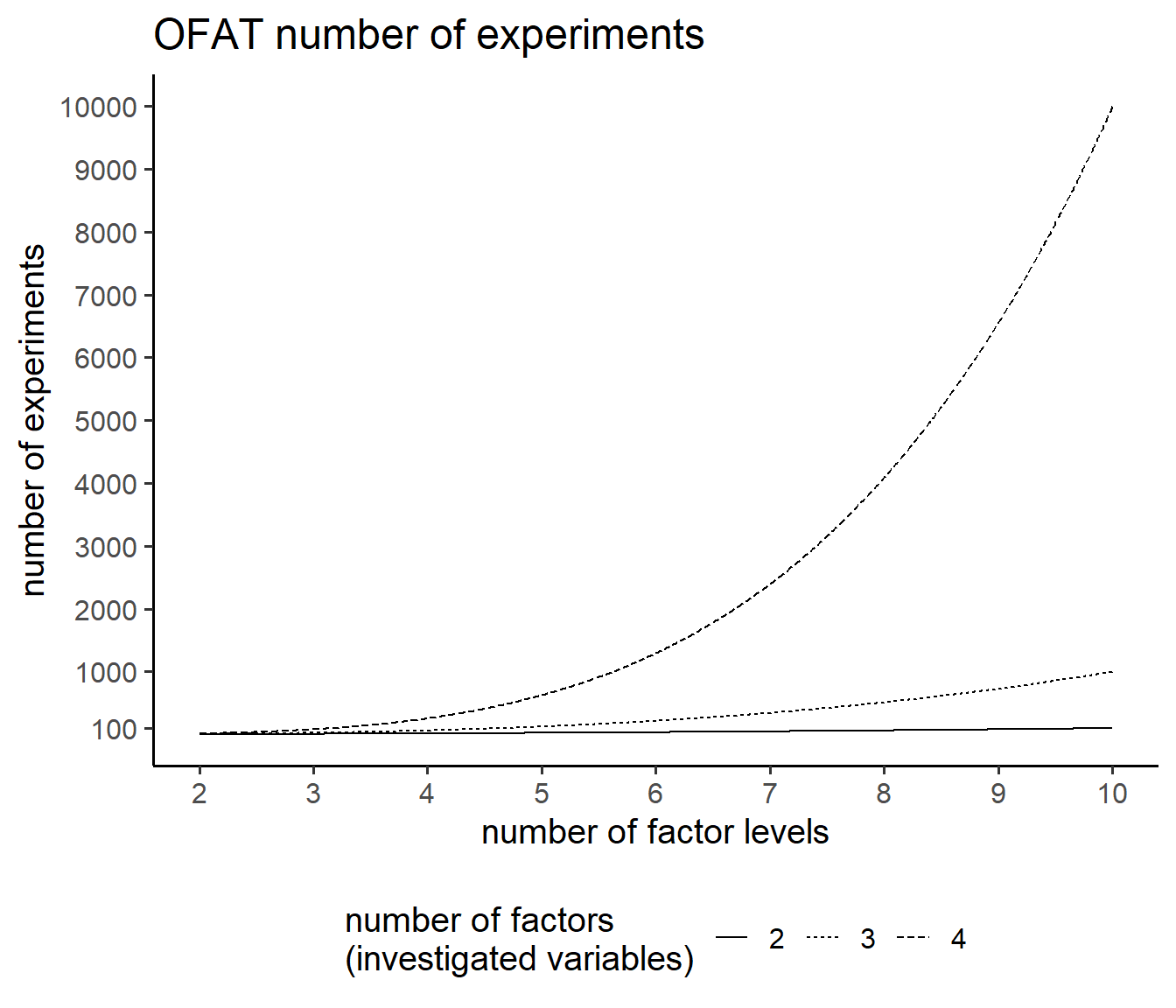
7.1 (O)ne (F)actor (A)t a (T)ime

Figure 7.1: OFAT quickly becomes cumbersome

7.2 curse of dimensionality

\[\begin{align} n_{experiments} = n_{levels}^{n_{factors}} \end{align}\]

7.3 Concept of ANOVA

Figure 7.2: classical ANOVA concept

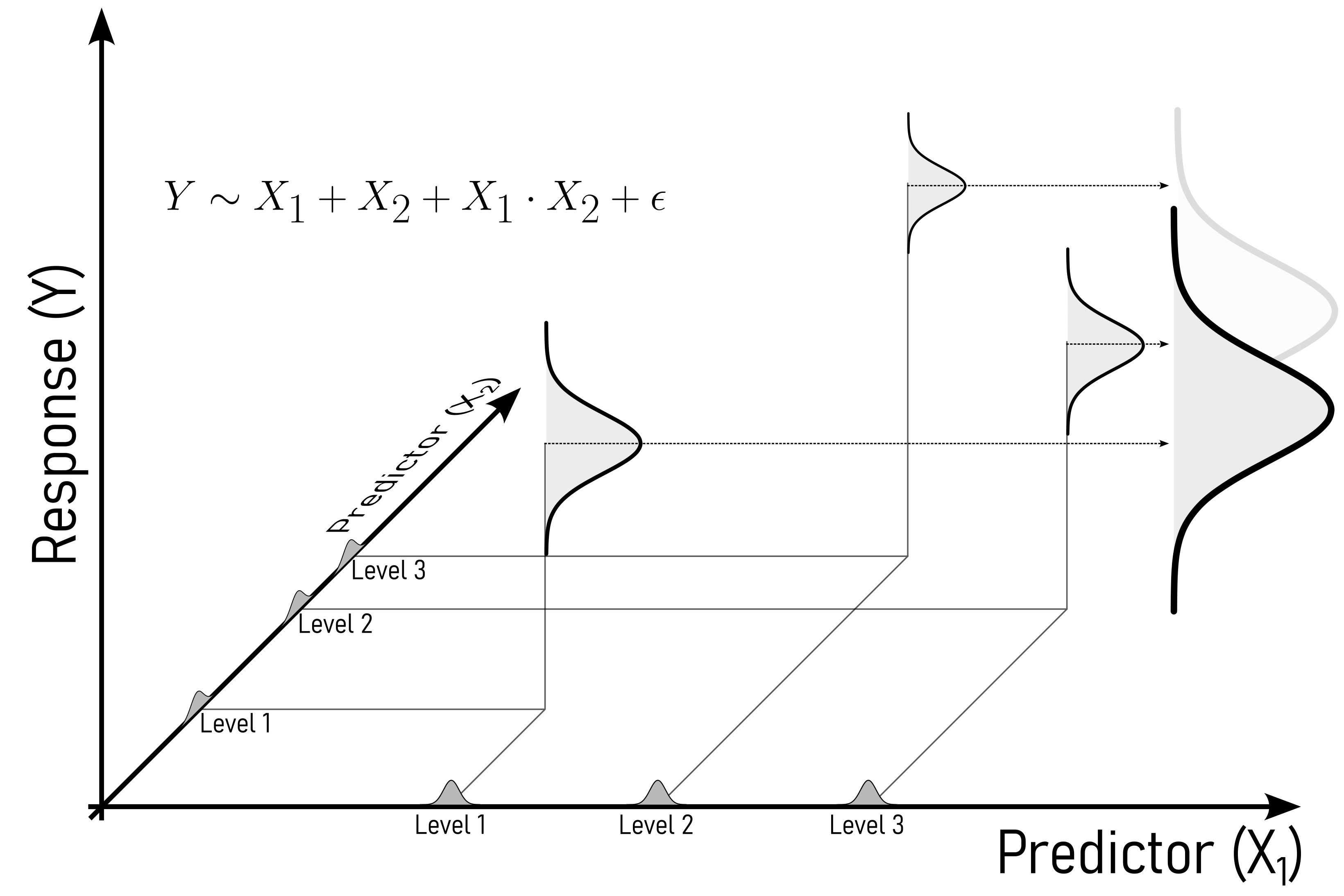
7.4 Basics of Experimental Design

Figure 7.3: The connection between ANOVA and DoE.

Design of Experiments (DoE)

7.5 Terminology

  • Factors (X’s): Independent variables (e.g., temperature, pressure, catalyst concentration).
  • Levels: Values a factor can take (e.g., low/high temperature).
  • Response (Y): Dependent variable (e.g., yield, defect rate).
  • Treatment: A specific combination of factor levels.
  • Replication: Repeating a treatment to estimate error.
  • Randomization: Assigning treatments randomly to reduce bias.
  • Blocking: Grouping similar experimental units to control nuisance variables.

7.6 Key Concepts

  • Factorial Designs: Study all combinations of factor levels (e.g., \(2^2 = 4 \text{runs}\) for \(2\) factors at \(2\) levels).
  • Main Effects vs. Interactions:
    • Main effect: Change in response due to one factor (e.g., increasing temperature increases yield).
    • Interaction: Effect of one factor depends on another (e.g., temperature and pressure interact to affect yield).
  • Orthogonality: Factors are uncorrelated (balanced designs).

7.7 DoE Types

7.7.1 Full Factorial

  • All possible combinations of factor levels are tested.
  • Example: 2 factors (A, B) at 2 levels → 4 runs (\(2^2\)).
  • Pros: Estimates all main effects and interactions.
  • Cons: Exponential growth in runs (e.g., 5 factors at 2 levels → 32 runs).

7.7.2 Fractional Factorial Designs

  • Subset of full factorial runs (e.g., ½ fraction of 2³ = 4 runs instead of 8).
  • Trade-off: Some interactions are confounded (aliased) with main effects.
  • Use case: Screening many factors to identify important ones.

7.7.3 Response Surface Methodology (RSM)

  • Goal: Model curvature (quadratic effects) to find optimal settings.
  • Designs: Central Composite Design (CCD), Box-Behnken.
  • Example: Optimizing yield by modeling temperature and pressure with quadratic terms.

7.7.4 Taguchi Methods

  • Focus: Robustness to noise (e.g., environmental variability).
  • Key idea: Use orthogonal arrays to minimize runs.
  • Criticism: Less flexible than classical DoE (fixed designs).

7.8 Steps in a DoE

Be bold, but not stupid

7.8.1 Define Objectives

  • Screening (identify important factors)?
  • Optimization (find best settings)?
  • Robustness (reduce variability)?

7.8.2 Select Factors & Levels:

Use subject-matter knowledge or preliminary experiments.

7.8.3 Choose Design

Full/fractional factorial? RSM? Taguchi?

7.8.4 Randomize & Run Experiments:

Avoid bias (e.g., time-order effects).

7.8.5 Analyze Data:

ANOVA, regression, effect plots.

7.8.6 Interpret & Validate:

  • Check assumptions (normality, independence).
  • Confirm with follow-up experiments.

7.9 Case Study - The catapult

7.9.1 Measurement System

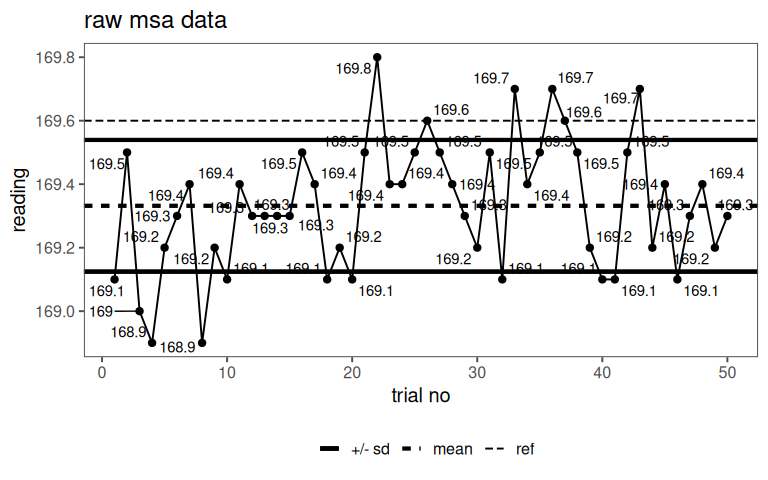
7.9.1.1 raw data

Figure 7.4: The MSA run chart.

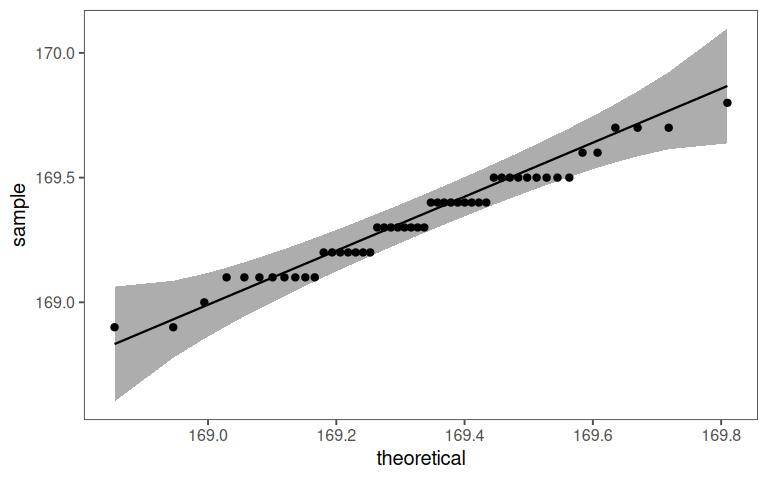
7.9.1.2 distribution

Figure 7.5: qq-plot of results

7.9.1.3 possible tolerance window

With a \(C_p = 2\) the tolerance window is \(\pm1.2cm\).

7.9.1.4 systematic error

.y. group1 group2 n statistic df p
tape_reading_cm 1 null model 50 -9.134823 49 3.72e-12

With a p-value of 3.72^{-12} there is a significant systematic error.

\[\begin{align} \epsilon_{\text{systematic}} = \text{reference}-\bar{x}_{\text{tape reading}} \end{align}\]

The systematic error is \(0.3cm\).

7.9.1.5 check experiment vs. tolerance window

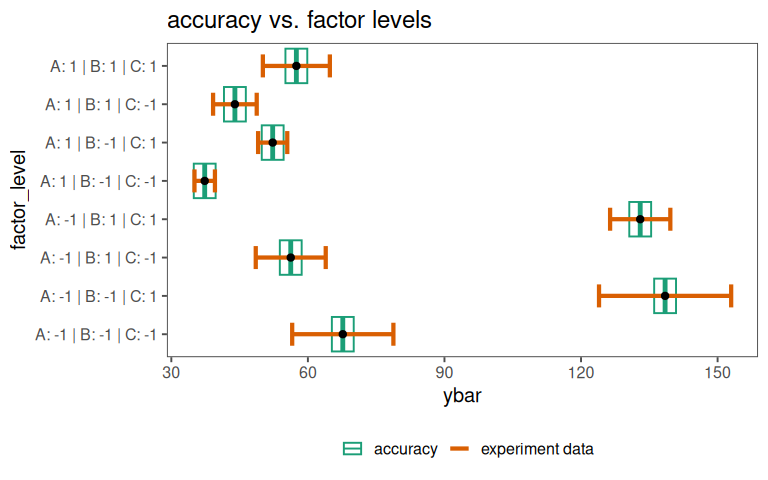
Figure 7.6: How good can the factor levels be measured?

7.9.2 Modeling

7.9.2.1 full model

7.9.2.1.1 model quality
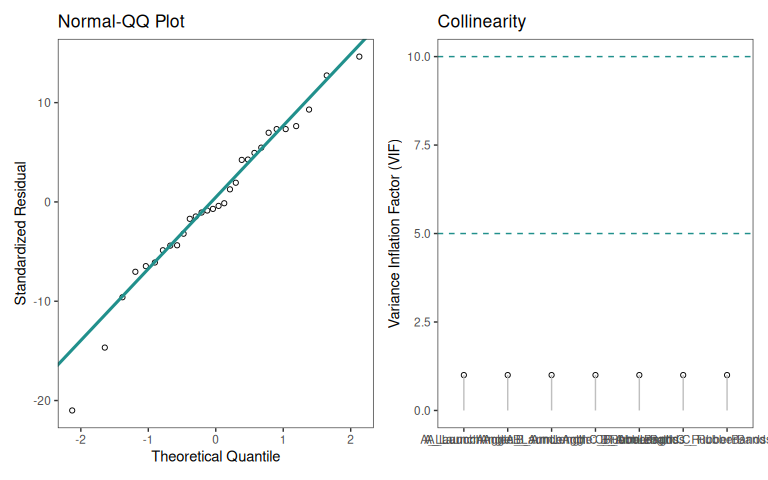
Figure 7.7: Model quality (including repetitions)
7.9.2.1.2 significance
Table 7.1: ANOVA results (full nmodel)
Characteristic Beta 95% CI p-value VIF
A_LaunchAngle -26 -29, -22 <0.001 1.0
B_ArmLength -0.63 -4.4, 3.1 0.7 1.0
C_RubberBands 22 18, 26 <0.001 1.0
A_LaunchAngle * B_ArmLength 3.6 -0.16, 7.3 0.060 1.0
A_LaunchAngle * C_RubberBands -15 -19, -11 <0.001 1.0
B_ArmLength * C_RubberBands 0.57 -3.2, 4.3 0.8 1.0
A_LaunchAngle * B_ArmLength * C_RubberBands -0.93 -4.7, 2.8 0.6 1.0
R² 0.950


Adjusted R² 0.934


Abbreviations: CI = Confidence Interval, VIF = Variance Inflation Factor

7.9.3 DoE - main modeling

7.9.3.1 pareto plot

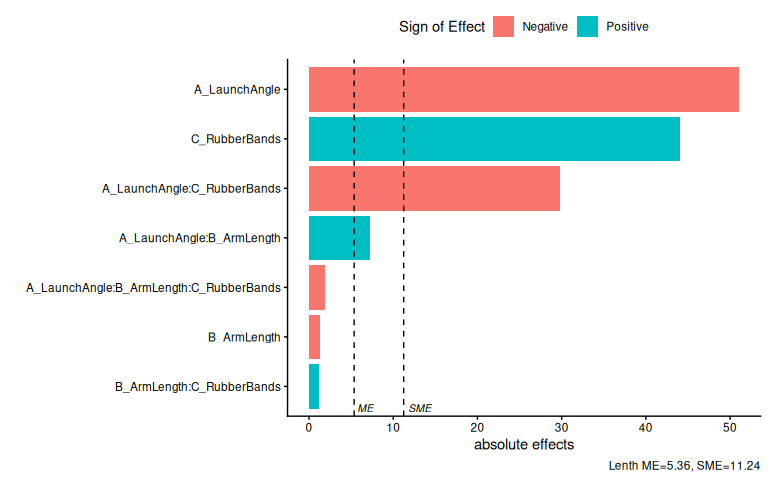
Figure 7.8: Pareto plot of parameters

7.9.3.2 half normal plot

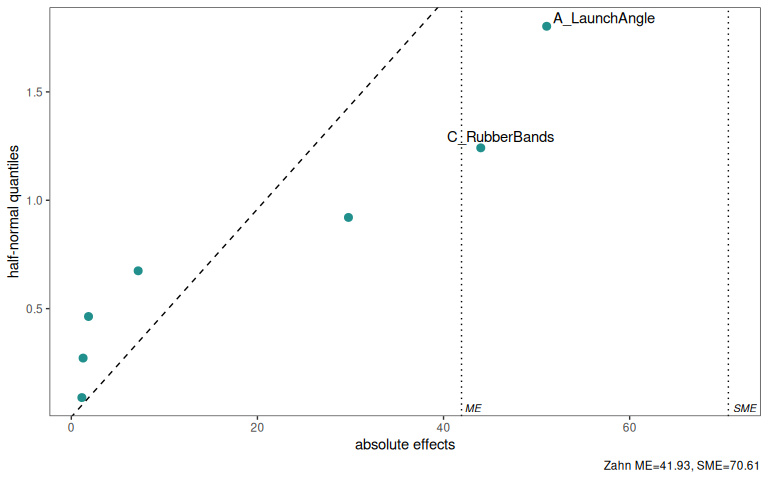
Figure 7.9: Half normal plot of parameters

7.9.3.3 Main effect plot

Figure 7.10: Main Effect plot

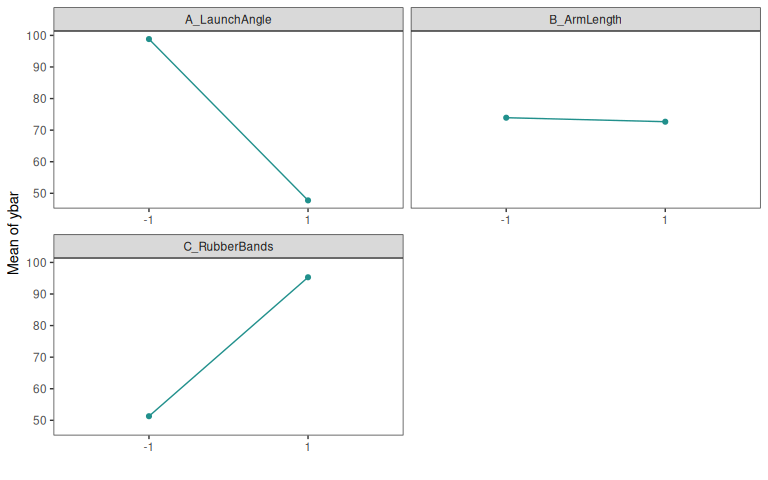
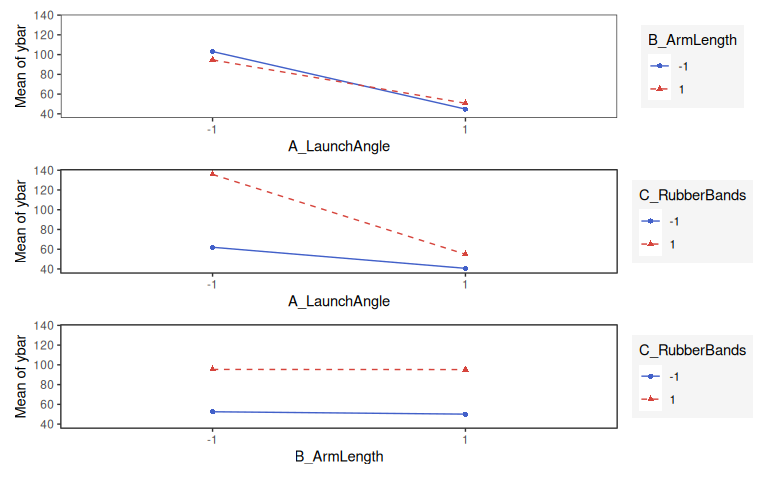
7.9.3.4 Interaction effect plot

Figure 7.11: Interaction plot

7.9.4 DoE - robust design

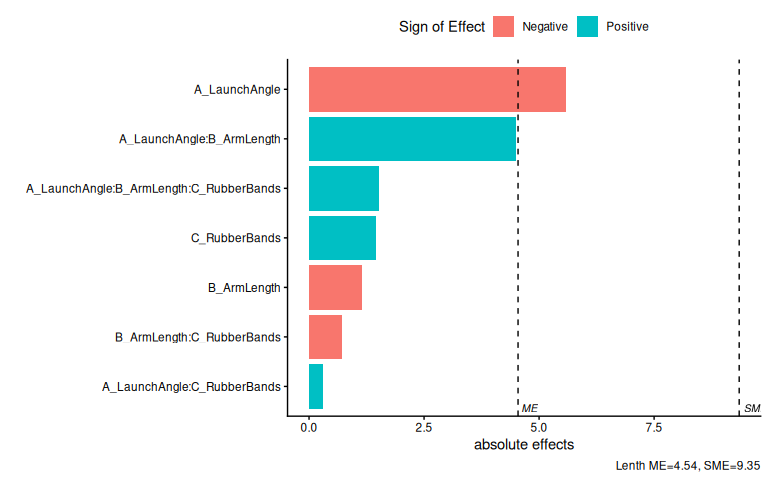
7.9.4.1 Pareto plot

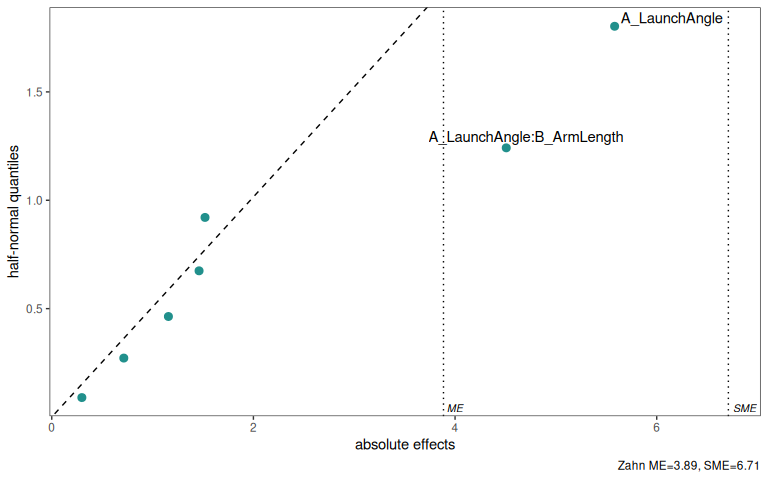
Figure 7.12: Pareto plot for robust design model

7.9.4.2 Half-normal plot

Figure 7.13: Half-normal plot for robust design model

7.9.4.3 Main effect plot

Figure 7.14: Main Effect plot

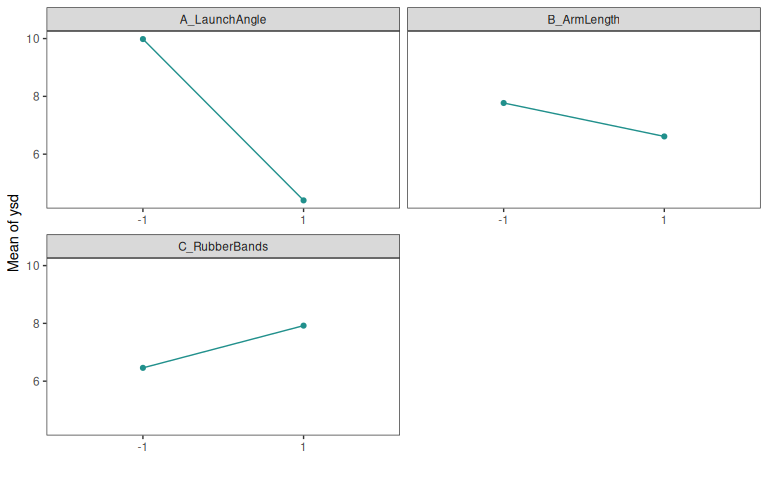
7.9.4.4 Interaction effect plot

Figure 7.15: Interaction plot

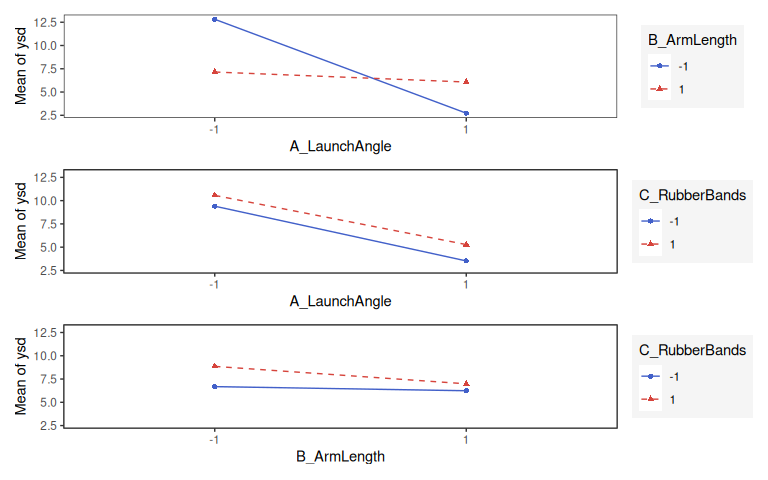
7.9.5 Check for linearity

7.9.5.1 Check center points

Figure 7.16: Interaction plot

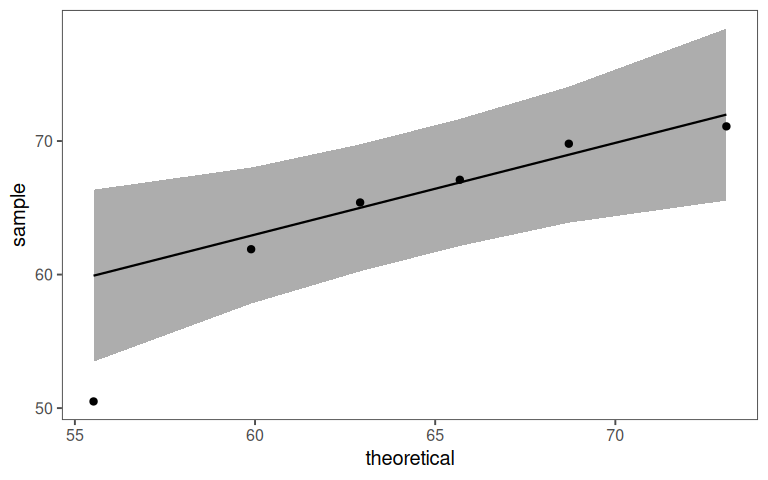
7.9.5.2 Test for linear model

Figure 7.17: Interaction plot

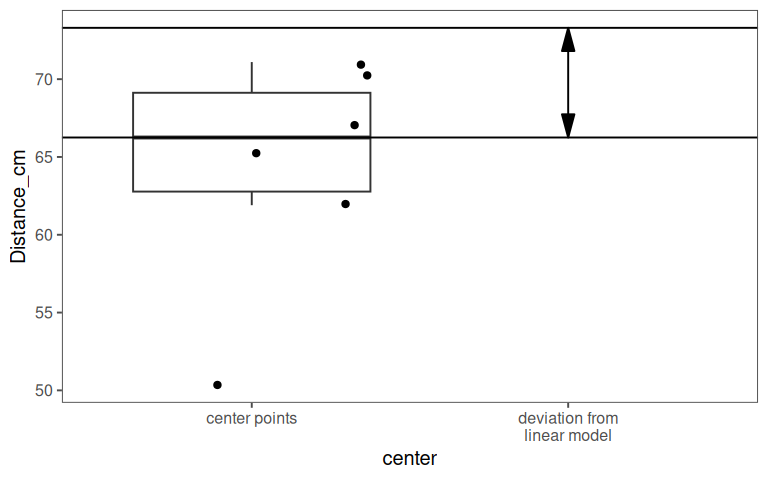
With a p value of \(0.032\) the center points deviate significantly from the linear model by about \(9cm\).

7.9.6 DoE - final model

7.9.6.1 Parameters - classic model

Table 7.2: Final DoE Model for Distance (dummy model)
Characteristic Beta 95% CI p-value VIF
A_LaunchAngle -26 -31, -20 <0.001 1.0
C_RubberBands 22 17, 27 <0.001 1.0
A_LaunchAngle * C_RubberBands -15 -20, -9.6 0.001 1.0
R² 0.989


Adjusted R² 0.982


Abbreviations: CI = Confidence Interval, VIF = Variance Inflation Factor

7.9.6.2 Parameters - robust design model

Table 7.3: Final DoE Model for robust design (dummy model)
Characteristic Beta 95% CI p-value VIF
A_LaunchAngle -2.8 -4.4, -1.2 0.008 1.0
B_ArmLength -0.58 -2.1, 0.98 0.4 1.0
A_LaunchAngle * B_ArmLength 2.3 0.69, 3.8 0.016 1.0
R² 0.913


Adjusted R² 0.847


Abbreviations: CI = Confidence Interval, VIF = Variance Inflation Factor

7.9.6.3 Final Catapult Model

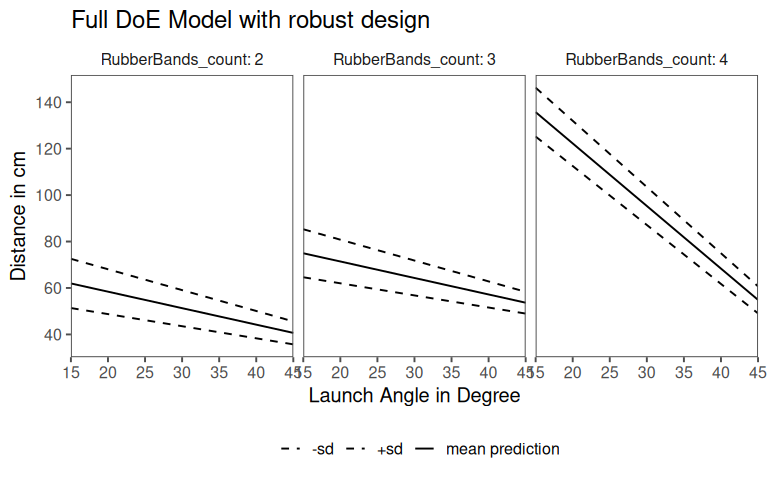
Figure 7.18: Visualization of final model including robust design

7.9.7 Fractional Factorial (Grömping 2014)

Goal: Identify main effects and key interaction with fewer experiments

7.9.7.1 Experimental plan

Original: \(2^3 \text{(factor levels)}* 3 \text{(repetitions)} + 6\text{(center points)} = 30 \text{ experiments}\)

Fractional (minimal): \(2^{3-1} \text{(factor levels)}* 1 \text{(no repetitions)} + 0\text{(center points)} = 4 \text{ experiments}\)

7.9.7.2 Aliasing

Figure 7.19: What is confounding?

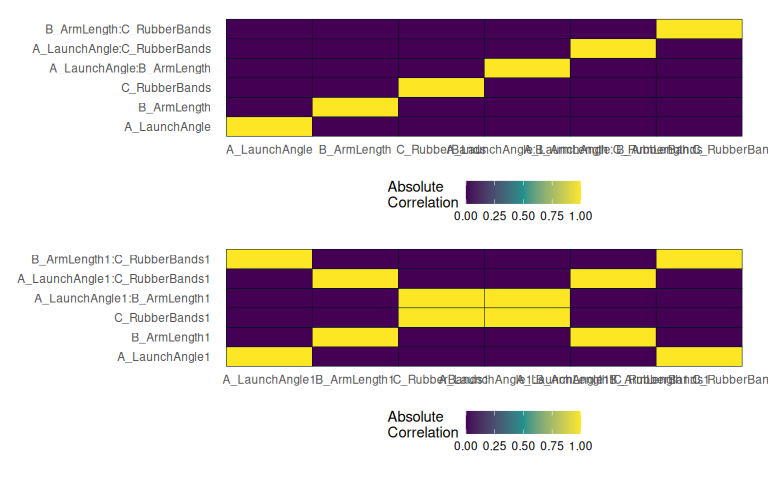
7.9.7.3 Confounding

Table 7.4: Example calculation to show what confounding means
A: Launch Angle B: Arm Length C: Rubber Bands A = B:C
-1 -1 1 -1
1 -1 -1 1
-1 1 -1 -1
1 1 1 1

7.9.7.4 Resolution

  • degree of confounding (or aliasing)
  • provides a way to classify designs based on how severely factors and interactions are confounded
  • Higher resolution means less confounding and more reliable estimation of effects
    • III: Main effects are confounded with two-way interactions
    • IV: Main effects are confounded with three-way (or higher) interactions, but two-way interactions are confounded with each other
    • V: Main effects and two-way interactions are confounded only with three-way (or higher) interactions.

7.9.7.5 practical implications

  • Lower resolution (e.g., R-III): Cheaper (fewer runs) but riskier because main effects may be confounded with two-way interactions.

If interactions exist, you might misinterpret the results.

  • Higher resolution (e.g., R-V): More expensive (more runs) but provides clearer estimates of main effects and two-way interactions.

Preferred when interactions are suspected or critical.

7.9.7.6 available designs and resoultion